inprogress which means I consider it largely incomplete in it's current state. Expect rough, unfinished thoughts.Contents
Spaced repetition is an evidence-based learning technique which utilizes the spacing effect. In contrast to more traditional repetition-based learning strategies such as cramming in which the main focus is on the total number of repetitions, spaced repetition is timing-based and focuses on maximizing efficiency by doing repetitions at scheduled times (typically decided by the difficulty of the material). Numerous studies have been conducted on spaced repetition (and on memory in general), and there is strong evidence suggesting that spaced repetition decreases the number of needed repetitions, and improves retention significantly over the long term. This article attempts to divulge into the specifics of spaced repetition implementations and the existing algorithms implemented in popular software like Anki, SuperMemo, Duolingo, and Quizlet. I will also share some general ideas and observations from the point of view of a daily user of spaced repetition.
A Quantitative Representation of Memory
Ebbinghaus (from self experiments) proposed an equation for the forgetting curve:
Where is the percentage of time saved on relearning (same thing as recall probability),
is the time in minutes, and
and
are constants. There are various reasons to discredit this specific equation, which I will not go into detail on. A quick summary: Ebbinghaus used nonsense syllables to test himself, which had little real world associations and coherence with past memories, and also measured with a comparatively short time interval of around 2 weeks, while spaced repetition is typically implemented well beyond that time period.
Thus, Ebbinghaus’s equation is usually dismissed in favour of one of exponential decay:
Where is the recall probability as a function of
(time), and
is the memory stability. The memory stability corresponds to how strong the memory is, specifically how much time it takes for the recall probability to decay to
. This is because when
, then
.
This equation seems to make logical sense. Consider the following cases:
- When
,
. This makes sense because
represents the initial retention rate when the item has just been reviewed, which should be 100%.
- When
(meaning we have reviewed the item a very long time ago):
(we have a retention rate of close to 0%).
- Another idea to consider is that
is not constant between repetitions of the same item. Each time the item is reviewed,
should grow because the item becomes more familiar with each repetition. Moreover, it would make sense for
to increase at an exponential rate because learning should compound over time1. In other words, as we do more and more repetitions,
, and when
, then
. This hypothetically means that after infinite repetitions, our recall probability will be 100%.
Looking at the equation, this means that in order to accurately predict the recall probability, the main hurdle is finding an accurate value for . The only other relevant variable is time
, which is easy to measure.
The value of (memory strength) is hard to predict and is influenced by a multitude of factors. Here are some I can think of from the top of my head, ranked from easiest to hardest to measure (from the algorithm’s perspective):
- Past reviews and performance on the same item, if the item was seen previously
- Difficulty of the material (subjective to individual differences)
- Format. How the material is presented.
- Previous experience and associations. More experience with similar material in the past will make future review easier. Also the degree of initial learning (Loftus, 1985)
- The current psychological and physical state of the user. Things like emotional disposition (Gumora & Arsenio, 20022) or consumption of caffiene (Cole, 20143). Sleep (Mirghani et al, 2015) especially seems to have large effects on memory strength. Motivation is obviously also a large factor.
Current Implementations
Most of the major implementations of scheduling algorithms that I think are relevent.
SM2 and other simple algorithms
Used by: Anki, Mnemosyne, Wanikani
Reference: SM2 (P. A.Wozniak, 1998)
SM2 is probably the most popular implementation of spaced repetition (and certainly the most decorated, despite it’s simplicity). In the algorithm, each review item is associated with an ease factor, which we hope to correspond to the difficulty of the review item. The original implementation consists of two initial hard coded learning phase steps: 1 day, and 6 days. Variants have other initial steps, and software like Anki allow customization of these.
A fairly simple formula is used to calculate subsequent intervals:
New interval = Previous interval * Ease factor
The ease factor is simply a floating point number between 1.3 and 2.5. It’s role, as seen in the formula, is to act as an interval multiplier leading to a larger and larger interval each time. The restrictions of 1.3 through 2.5 attempt to keep the number of repetitions reasonable. An ease below 1.3 will lead to the material being studied too often (usually indicative not because the knowledge itself is too difficult, but because it is poorly formatted or presented), and anything greater than 2.5 will space the intervals too much, especially as they get larger.
At larger intervals, even 2.5 may be too much, and this will infinitely grow. This is why most software using this provide a top interval cap. Capping at around 10 months to a year sounds like a reasonable interval. Once a review item hits the cap, each review would presumably increase memory utility by a relatively large amount because the time interval is so big, and with hardly any extra time investment, so growing the interval further leads to diminishing returns. In most implementations, the ease factor is adaptive to lowering as well. For example in Anki by default, if a user answers incorrectly, then the ease is decreased by 20%.
Wanikani uses an alternate version of SM2 with predetermined ease factors and with intervals represented by levelling up of stages, which is less flexible but does the job.
Regression based on Recall Probability
The first thought I had when pondering on algorithms for spaced repetition is using a simple logistic regression classifier (trained on the user’s previous data) to output a probability that the user will get the review item right given an input of the time interval. We can use this recall probability in numerous ways, Quizlet uses it to order the items for review (items with lower recall probability are reviewed first).
My thoughts were that the user could choose a desired recall probability (we’ll call this the ‘recall threshold’ for now), which corresponds to the decision threshold of the classifier. A recall threshold of around 80% makes sense (of course, this will vary with different individuals). The algorithm will show the item once the recall threshold for it falls below 80%. In order to accurately predict the recall probability, this classifier would be trained on features based on past couple repetitions of the same item (Quizlet uses the past 3). It would check to see if the prior attempts were correct, how quickly they were answered, and how many consecutive attempts were correct, which will all help predict the classifier predict the probability of answering the current attempt correctly. Of course, the difficulty of the material is a large factor (that Quizlet apparently doesn’t use), but difficulty is different for different individuals, which is why other algorithms like the SuperMemo family ask the user to rate how easy the item was to answer and uses that rating when considering further intervals. This does require more cognitive load from the user, which can be ameliorated at the cost of accuracy by having the algorithm automatically assign the rating based on factors like the time taken to answer, or at least provide a suggested score based on such factors.
Duolingo models its ‘half-life regression’ approach very similar to the forgetting curve equation described above:
is the probability of recall
is the time since the item was last reviewed
is the half life corresponding to the learner’s memory strength. The value of this is hoped to correspond with the amount of time it takes the recall probability to decay to 0.5, or 50%. This is because when
, the equation evaluates to
.
should increase exponentially with every repetition (this is analogous to the
memory strength value), and thus can be modeled by in the form
. Duolingo assumes 2 as the base:
is a vector of parameters and
is a vector of features. This is now a typical regression problem. All we need is a dataset from previous review performance consisting of the recall rate
, the time since last review
, and the values for each of the feature vector
. Duolingo used the following features: the total number of times the user has seen the item before, the number of times the item was answered correctly and incorrectly, and a large set of lexeme tags indicating the difficulty of each item. The predicted recall rate can be calculated by using
, and a loss function can be constructed by comparing the predicted value with the actual measured recall rate from our dataset. We can then find values of
that minimize this loss function. I won’t go into detail about all of this, check the Duolingo paper linked above for the full equations, apparently they also decided to factor an approximation of
in the cost function. It seemed to provide decent results, the following image shows an attempt for the algorithm to fit curves for the predicted recall rate based on the forgetting curve from data points (the black ‘x’ marks):
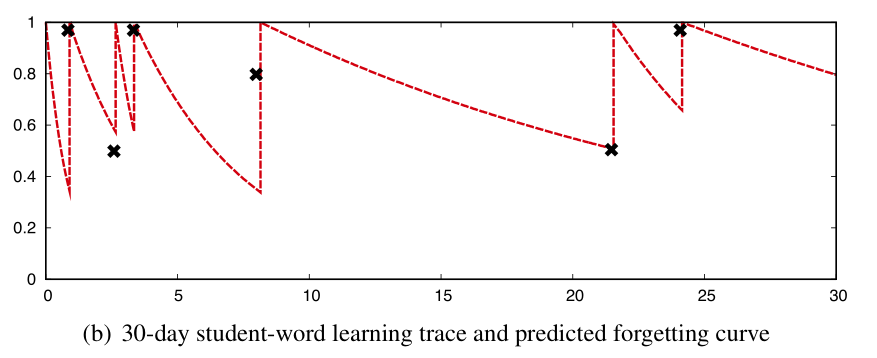
(Settles & Mender, 2016)
Further Reading
Interesting studies, articles, and links I read (or at least skimmed) when researching the topic.
- Improving Students' Learning With Effective Learning Techniques: Promising Directions From Cognitive and Educational Psychology (J. Dunlosky et al. 2013)
- Memory: A Contribution to Experimental Psychology (H. Ebbinghaus, 1885) Translated from German
- Studies on the forgetting curve, effects of various elements, attempts at quantifying:
- The form of the forgetting curve and the fate of memories (L. Averell and A. Heathcote, 2011) [ scihub link]
- The Precise Time Course of Retention (D. Rubin, S. Hinton, and A. Wenzel, 1999) [scihub link]
- Forgetting curves in long-term memory: Evidence for a multistage model of retention (M. Fioravanti and F. Cesare, 1992) [scihub link]
- Evaluating Forgetting Curves (G. R. Loftus, 1985)
- Jost’s Law, cited in another paper on retrograde amnesia (J. T. Wixted, 2004)
Implementations
Duolingo’s algorithm: A Trainable Spaced Repetition Model for Language Learning (B. Settles & B. Mender, 2016) [Github]
SuperMemo-based (only major versions):
Learning compounds over time, or at least should, in theory. This is because at the beginning stages of learning something unfamiliar, an individual has no pre-existing schema of the concept. As they spend time with the material, they will develop some sort of a schema for the concept, which will help them better understand related concepts in the future. ↩︎
scihub link (G. Gumora & W. F. Arsenio, 2002, Emotionality, Emotion Regulation, and School Performance in Middle School Children) ↩︎
scihub link (J. S. Cole, 2014, A survey of college-bound high school graduates regarding circadian preference, caffeine use, and academic performance) ↩︎
Quizlet doesn’t implement true spaced repetition because it’s designed for cramming. It doesn’t have a strict scheduler and focuses primarily on the order of review, with higher priority items (ones with lower recall probability) being shown first. Quizlet does have a ‘Long-Term Learning’ mode with a scheduler that appears to follow a fixed formula of
new interval = (old interval * 2) + 1with new items starting at a 1 day interval. Items answered incorrectly are reset to the same status as new items. Of course, this is less than optimal as the fixed rate multiplier assumes that all material is the same difficulty. ↩︎